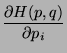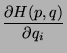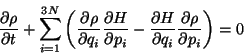Next: Micro-canonical Ensemble
Up: ensemble
Previous: ensemble
Consider an isolated system with unchanging  .
.
Figure:
Phase Space
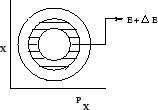 |
Phase Space - The 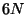 -dimensional space defined by the
-dimensional space defined by the 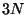 canonical
co-ordinates and
canonical
co-ordinates and 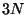 canonical momenta. In this space
canonical momenta. In this space 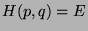 defines an
energy surface. An energy conserving (isolated) system always stays on the same
surface. A system defined by
defines an
energy surface. An energy conserving (isolated) system always stays on the same
surface. A system defined by
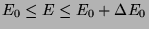 occupies a region
like the shaded one in the phase-space shown in figure[1]. The dynamics of
the system is completely determined by the set of
occupies a region
like the shaded one in the phase-space shown in figure[1]. The dynamics of
the system is completely determined by the set of 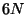 equations of motion, given by,
equations of motion, given by,
where 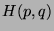 is the Hamiltonian of the system. The phase-space density function,
is the Hamiltonian of the system. The phase-space density function,
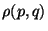 , is defined such that
, is defined such that
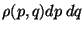 is the number of representative
points contained in the volume
is the number of representative
points contained in the volume 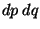 located at
located at 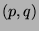 in the phase-space (denoted
by
in the phase-space (denoted
by 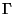 ).
).
Lioville's Theorem - The local density of representative points in the phase-space
remain the same for an observer moving with a point. In other words, the distribution of the
phase-space points move like an incompressible fluid. This implies,
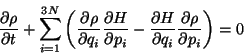 |
(3) |
If
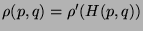 then
then
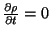 , i.e, the
density of states is time-independent. A particular class of choice, in which
, i.e, the
density of states is time-independent. A particular class of choice, in which 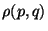 is constant (equal a priori probability), gives the micro-canonical ensemble. This
is evident for systems with a constant energy.
is constant (equal a priori probability), gives the micro-canonical ensemble. This
is evident for systems with a constant energy.
Postulate of Equal a Priori Probability - All the microscopic states corresponding
to a particular macroscopic state of a system in thermal equilibrium are equally likely.
Consequence - Any macroscopic state in thermodynamic equilibrium is a member of
the micro-canonical ensemble with the density function,
Ensemble Average of any macroscopic quantity 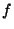 is defined as,
is defined as,
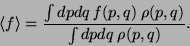 |
(6) |
The ensemble average is very close to the most probable value if the fluctuation
is small. The mean square deviation of 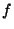 is given by,
is given by,
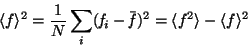 |
(7) |
and, therefore, the fluctuation is given by,
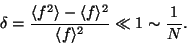 |
(8) |
Hence, for large 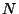 the average value is equal to the most probable value.
The Postulate of Classical Statistical Mechanics is established experimentally.
The logical justification actually comes from Quantum Mechanics.
the average value is equal to the most probable value.
The Postulate of Classical Statistical Mechanics is established experimentally.
The logical justification actually comes from Quantum Mechanics.
Subsections
Next: Micro-canonical Ensemble
Up: ensemble
Previous: ensemble
Sushan Konar
2004-08-19
![]() .
.