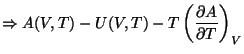Next: Grand Canonical Ensemble
Up: Classical Statistical Mechanics
Previous: Micro-canonical Ensemble
This approach is suitable for a system which is mechanically isolated but is in contact
with a heat bath. Therefore such a system is defined by a fixed number of particles and
a fixed volume. And the system is kept at a constant temperature through its interaction
with the environment. Therefore, the energy of the system is variable.
Consider a mechanically and thermally isolated system (can be treated using the Micro-canonical
Ensemble Approach) defined by 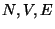 . Consider two subsystems in thermal contact defined by
. Consider two subsystems in thermal contact defined by
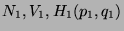 and
and
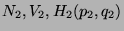 . Then, if each of the subsystem has a
small variation in energy given by
. Then, if each of the subsystem has a
small variation in energy given by 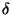 ,
,
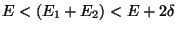 . Although this
includes a range of values for
. Although this
includes a range of values for 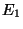 and
and 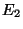 , we have seen in the previous section that only
one set of values
, we have seen in the previous section that only
one set of values
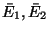 are important. Assume
are important. Assume 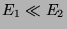 . Let
. Let 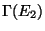 be
the phase-space volume corresponding to the subsystem 2. The probability of finding system 1
within
be
the phase-space volume corresponding to the subsystem 2. The probability of finding system 1
within 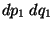 of
of 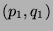 regardless of system 2, is proportional to
regardless of system 2, is proportional to
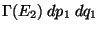 ,
where
,
where 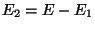 . Therefore, upto a proportionality constant,
. Therefore, upto a proportionality constant,
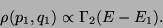 |
(38) |
Now, since, 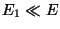
Since, 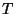 is the equilibrium temperature for both the subsystems. Therefore,
is the equilibrium temperature for both the subsystems. Therefore,
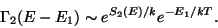 |
(40) |
Therefore, for the smaller subsystem, we have,
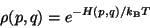 |
(41) |
where 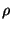 is normalised. Now, this smaller subsystem can be treated as a system in mechanical
isolation but in thermal contact with the environment. Therefore, the phase-space density of such
a system is given by the above relation. So, the Canonical Ensemble approach is defined by this
phase-space density, where
is normalised. Now, this smaller subsystem can be treated as a system in mechanical
isolation but in thermal contact with the environment. Therefore, the phase-space density of such
a system is given by the above relation. So, the Canonical Ensemble approach is defined by this
phase-space density, where 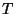 is defined through the contact with a heat bath.
is defined through the contact with a heat bath.
The phase-space volume, known as the Partition Function is given by,
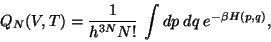 |
(42) |
where,
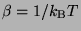 . It should be remembered that the integration over
. It should be remembered that the integration over 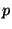 is such that
all possible values of
is such that
all possible values of 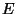 are allowed. However, only one value of
are allowed. However, only one value of 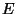 contributes to the integral
overwhelmingly (this is the mean or average energy). The connection with thermodynamics is established
through the relation,
contributes to the integral
overwhelmingly (this is the mean or average energy). The connection with thermodynamics is established
through the relation,
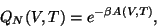 |
(43) |
where, 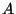 is the Helmholtz free energy.
is the Helmholtz free energy.
Once again, we need to identify 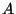 defined thus with its thermodynamics properties. Therefore,
we must prove that,
defined thus with its thermodynamics properties. Therefore,
we must prove that,
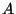 is extensive - If the interaction between the two subsystems (mutually exclusive) is negligible
compared to the total energy of either of them, then evidently
is extensive - If the interaction between the two subsystems (mutually exclusive) is negligible
compared to the total energy of either of them, then evidently 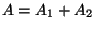 .
.
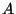 is related to
is related to
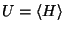 and
and
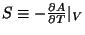 through the relation
through the relation 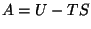 .
.
For the second condition, let us start with the definition of 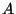 through the partition function.
through the partition function.
Therefore, the recipe for thermodynamics using Canonical Ensemble Approach is given by,
The other thermodynamic variables like pressure or entropy are obtained the usual way, like,
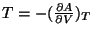 ,
,
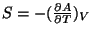 and so on. The ensemble average of energy is given by,
and so on. The ensemble average of energy is given by,
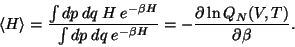 |
(45) |
Similarly, the mean square fluctuation of energy is given by,
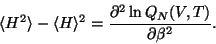 |
(46) |
Next: Grand Canonical Ensemble
Up: Classical Statistical Mechanics
Previous: Micro-canonical Ensemble
Sushan Konar
2004-08-19
![]() . Consider two subsystems in thermal contact defined by
. Consider two subsystems in thermal contact defined by
![]() and
and
![]() . Then, if each of the subsystem has a
small variation in energy given by
. Then, if each of the subsystem has a
small variation in energy given by ![]() ,
,
![]() . Although this
includes a range of values for
. Although this
includes a range of values for ![]() and
and ![]() , we have seen in the previous section that only
one set of values
, we have seen in the previous section that only
one set of values
![]() are important. Assume
are important. Assume ![]() . Let
. Let ![]() be
the phase-space volume corresponding to the subsystem 2. The probability of finding system 1
within
be
the phase-space volume corresponding to the subsystem 2. The probability of finding system 1
within ![]() of
of ![]() regardless of system 2, is proportional to
regardless of system 2, is proportional to
![]() ,
where
,
where ![]() . Therefore, upto a proportionality constant,
. Therefore, upto a proportionality constant,
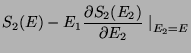
![]() defined thus with its thermodynamics properties. Therefore,
we must prove that,
defined thus with its thermodynamics properties. Therefore,
we must prove that,
![$\displaystyle \frac{\partial}{\partial \beta}
\frac{1}{h^{3 N}} \int dp dq e^{\beta [ A(V, T) - H (p, q)]}$](img163.png)
![$\displaystyle \frac{1}{N!h^{3N}} \int dp dq e^{\beta [A( v, T ) - H (p, q)]...
...T) - H(p, q) + \beta \left(\frac{\partial A }{\partial \beta} \right)_V \right]$](img165.png)