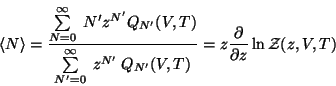Next: About this document ...
Up: Classical Statistical Mechanics
Previous: Canonical Ensemble
So, far we have considered systems which are isolated (either completely or at least mechanically).
Let us now consider more realistic systems which are in neither mechanically nor thermally isolated.
In other words, in this section we shall deal with systems which are in thermal contact with a heat
bath (so that the temperature is kept constant) and also exchanges particles with the environment
(with the chemical potential kept constant). Therefore, now the 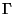 -space comprises of all the
canonical momenta and co-ordinates of systems with 0, 1, 2, ..,
-space comprises of all the
canonical momenta and co-ordinates of systems with 0, 1, 2, .., 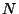 particles. And the phase-space
density
particles. And the phase-space
density 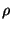 is a function not only of (
is a function not only of (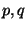 ) but of
) but of 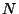 as well.
as well.
Consider a mechanically isolated system in contact with a heat bath (so that the system can be
treated using Canonical Ensemble Approach) defined by 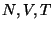 . Consider two subsystems of this
which can exchange energy, as well as particles defined by
. Consider two subsystems of this
which can exchange energy, as well as particles defined by 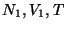 and
and 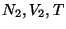 . Then,
. Then,
Let us assume that 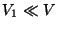 and
and 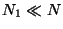 . Then, neglecting the inter-particle interactions
across the surface separating the two subsystems, we have,
. Then, neglecting the inter-particle interactions
across the surface separating the two subsystems, we have,
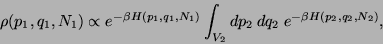 |
(47) |
where, 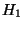 and
and 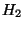 have the same functional form. Choosing appropriate proportionality constants, we have,
have the same functional form. Choosing appropriate proportionality constants, we have,
so that,
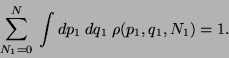 |
(49) |
Now,
and,
where,
We define the Grand Partition Function to be,
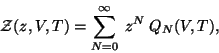 |
(52) |
where,
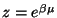 and
and 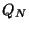 is the Partition function of a system with
is the Partition function of a system with 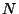 particles.
Since,
particles.
Since,
we have,
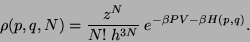 |
(53) |
The recipe for thermodynamics is given by
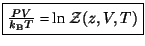 .
and,
.
and,
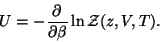 |
(54) |
Alternatively,
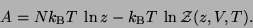 |
(55) |
The ensemble average of the particle number is given by,
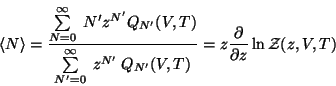 |
(56) |
Similarly, the mean square fluctuation of the number of particles is given by,
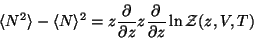 |
(57) |
Next: About this document ...
Up: Classical Statistical Mechanics
Previous: Canonical Ensemble
Sushan Konar
2004-08-19
![]() -space comprises of all the
canonical momenta and co-ordinates of systems with 0, 1, 2, ..,
-space comprises of all the
canonical momenta and co-ordinates of systems with 0, 1, 2, .., ![]() particles. And the phase-space
density
particles. And the phase-space
density ![]() is a function not only of (
is a function not only of (![]() ) but of
) but of ![]() as well.
as well.
![]() . Consider two subsystems of this
which can exchange energy, as well as particles defined by
. Consider two subsystems of this
which can exchange energy, as well as particles defined by ![]() and
and ![]() . Then,
. Then,
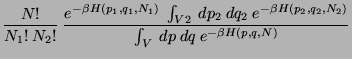
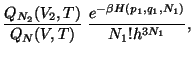
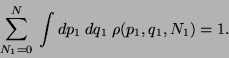
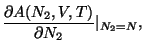
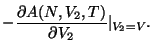
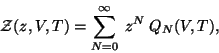
![]() .
and,
.
and,