Quantum Mechanics I : Final Examination
General Instructions
- Attempt all 20 problems.
- All carry the same mark.
- You can use calculators but order-of-magnitude answers are also acceptable.
- No lengthy calculation is required.
- Prove that isotropy of space is equivalent to the condition
![$[H, L] = 0$](img1.png) .
.
- Show that
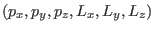 are closed with respect to
commutation (i.e., commutation between two elements of the set produces another
element of this same set). This set forms a Lie-group, known as the
Euclidean group
are closed with respect to
commutation (i.e., commutation between two elements of the set produces another
element of this same set). This set forms a Lie-group, known as the
Euclidean group 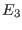 in 3-D.
in 3-D.
- Do the hydrogen atom energy levels get modified significantly at the surface
of a Neutron Star?
- A recently discovered class of Neutron Stars have a surface magnetic field of
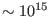 G. These are known as Magnetars. Find the Zeeman splitting of
the (
G. These are known as Magnetars. Find the Zeeman splitting of
the (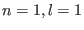 ) state of hydrogen atom near a Magnetar.
) state of hydrogen atom near a Magnetar.
- The ionised hydrogen regions of Interstellar medium are known as HII region.
The HII region formed around a bright star is known as the Stromgren Sphere.
Find the radius of the Stromgren Sphere centred around a star of radius
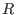 and
surface temperature
and
surface temperature 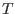 where the density of interstellar medium is
where the density of interstellar medium is 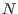 .
.
-
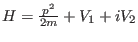 , where
, where 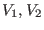 are real. Show that the
probability is not conserved but has a source/sink.
are real. Show that the
probability is not conserved but has a source/sink.
- Quantise the system consisting of two neutral particles of masses equal to
those of electron and proton held together by gravity. Obtain the expression for
the energy eigenvalues.
- Show that in the limit
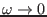 the harmonic oscillator wave-functions
approach free-particle limit.
the harmonic oscillator wave-functions
approach free-particle limit.
- Two particles of equal mass are placed in the potential
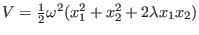 . Find the energy eigenvalues.
. Find the energy eigenvalues.
- Show that the Laplace-Runge-Lenz vector
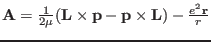 is a constant motion for hydrogen atom.
is a constant motion for hydrogen atom.
- Find the zero point of the following system - a mass of
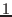 gm is connected to a fixed point
by a spring which is stretched by
gm is connected to a fixed point
by a spring which is stretched by 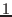 cm when subjected to a force of
cm when subjected to a force of 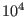 dyne. The mass point
is forced to move only in one direction.
dyne. The mass point
is forced to move only in one direction.
- For
![$[a, a^{\dagger}] = 1$](img16.png) prove that
prove that
![$[a^{\dagger}a, a] = -a$](img17.png) and
and
![$[a^{\dagger}a, a^{\dagger}] = a^{\dagger}$](img18.png) .
Show that with
.
Show that with
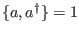 the above relations would still be valid but the number operator
the above relations would still be valid but the number operator
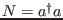 now has the eigenvalues 0 and 1. As you might have guessed, the former case refers
to the Bosons and the latter to the Fermions in the second-quantised formulation.
now has the eigenvalues 0 and 1. As you might have guessed, the former case refers
to the Bosons and the latter to the Fermions in the second-quantised formulation.
-
![$J_{+/-} = J_x +/- i J_y, [J_+, V+] = 0, [J_z, V_+] = V_+$](img21.png)
If 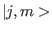 are the simultaneous eigenstates of
are the simultaneous eigenstates of 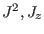 then show that
then show that
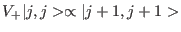 .
.
-
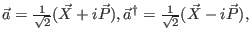
where,
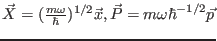 . Show that
. Show that
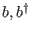 change the angular momentum by one unit, whereas
change the angular momentum by one unit, whereas 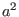 changes the energy by one unit,
where
changes the energy by one unit,
where
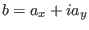 and
and
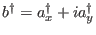 .
.
- Consider a relativistic electron with
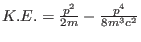 . Assuming the
extra term to be a perturbation show that the modification to the Hydrogen atom energy levels is given
by
. Assuming the
extra term to be a perturbation show that the modification to the Hydrogen atom energy levels is given
by
![$\Delta E = \left[ \frac{3}{8n^4} - \frac{1}{(2l+1)n^3}\right] \frac{me^4}{\hbar^2} (\frac{e^2}{\hbar c})^2$](img32.png)
- A mono-energetic beam of particles is incident on a set of N identical static potentials. Show that
the differential cross-section in the lower Born-approximation is
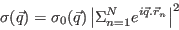 |
(1) |
where 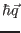 is the momentum transfer on collision,
is the momentum transfer on collision,
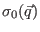 is the cross-section
for scattering off one potential and
is the cross-section
for scattering off one potential and 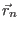 is the centre of the nth potential.
is the centre of the nth potential.
- Consider the perturbation
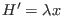 over a 1-D harmonic oscillator potential.
Find the change in the ground state energy. What happens if
over a 1-D harmonic oscillator potential.
Find the change in the ground state energy. What happens if
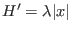 ?
?
- Consider a hydrogen atom fixed at the origin. Two charges
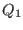 and
and 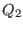 are placed on z-axis,
at
are placed on z-axis,
at 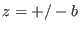 where
where 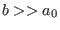 and
and 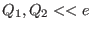 . What can be said about the states when
. What can be said about the states when
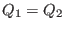 and
and 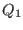 not equal to
not equal to 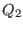 ?
?
- Consider an alkali atom placed in an external magnetic field. Find the minimum value of the
magnetic field when the spin-orbit coupling term and Zeeman term in the Hamiltonian becomes equal.
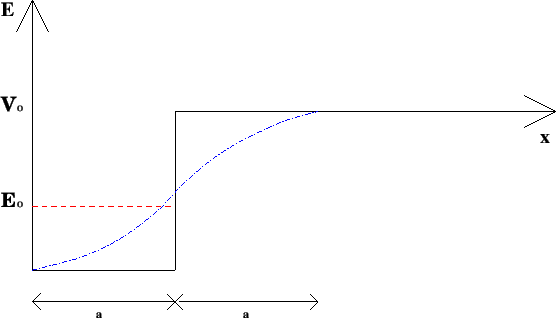
- A half-square-well potential is smoothed at the edges symmetrically, as shown in fig.(
![[*]](/usr/share/latex2html/icons/crossref.png) ) .
How would the energy
) .
How would the energy 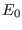 of the bound state change under such modification of the potential?
of the bound state change under such modification of the potential?
Figure:
Question No. 20
 |