Mid-Semester Examination
total marks - 50, time - 2 hours
Physical & Astrophysical Data :
Special Instruction : Calculators are not to be used.
Multiple Choice : 1 x 10 = 10
- Equatorial mounting is the most special characteristic of the radio telescope at
- Gauribidanur (near Bangalore)
- Hanle
- Narayangaon (near Pune)
- Ooty
- Radiation in UV band is characteristic of
- atomic binding energy
- molecular binding energy
- nuclear energy
- rest mass energy
- In order to use the window grill in this room as a diffraction grating
- a sodium vapour lamp
- a fusion reactor
could be an appropriate source of radiation.
- Thermal Bremsstrahlung is
- radiation emitted by electrons scattered by other electrons
- radiation emitted by electrons scattered by heavier ions
- radiation emitted by electrons accelerated by a magnetic field
- radiation emitted by level transitions of atomic electrons
- The minimum mass for an object to be gravitationally bound is
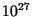 gm
gm
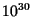 gm
gm
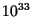 gm
gm
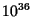 gm
gm
- The same side of Mercury faces the Sun always. The spin period of Mercury is
- larger than
- smaller than
- equal to
- not related to
its orbital period.
- What does the Hertzsprung-Russel diagram represent?
- This is a plot of luminosity over surface temperature of stars.
- One can extract the evolutionary tracks of stars.
- One can extract the evolution of black holes in time.
- One can learn something about the space-time structure of compact objects
with these diagrams.
- After exhausting its nuclear fuel the Sun would end its life as a
- neutron star
- He white dwarf
- C-O white dwarf
- type-I supernova, leaving no remnant
- Photo-disintegration of a nucleus requires temperatures in excess of
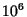 K
K
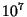 K
K
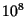 K
K
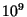 K
K
- The phenomenon of neutron drip happens at a density of
-
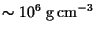
-
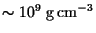
-
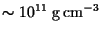
-
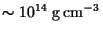
Short Questions (Any 10) : 3 x 10 = 30
- Prove that the atoms even on the surface (
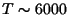 K) of the Sun are ionised.
K) of the Sun are ionised.
- During WWII a squadron of fighter planes would typically take off or land against the
setting / rising Sun (You may have seen this in a Hollywood war movie.). Apart from the
view being quite breathtaking what was the technical reason behind this?
- State the assumptions under which a gas of particles, interacting only through collisions,
could be assumed to be in thermal equilibrium.
- The average temperature of the earth is
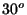 C. What is the typical wavelength at which
the thermal radiation from the earth would be maximum?
C. What is the typical wavelength at which
the thermal radiation from the earth would be maximum?
- Calculate the classical electron radius.
- Let us assume that a space-ship is built in orbit, beyond the atmosphere of the earth.
The major fuel requirement of such a ship would be for a) propulsion, b) heating. What
would be the most fuel efficient shape of this space-ship and why?
- Communication and weather satellites are often placed in geosynchronous or 'parking'
orbits. At what altitude must they be located?
- Calculate the Larmor radius of electrons with average kinetic temperature of
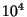 K
in presence of a magnetic field of
K
in presence of a magnetic field of
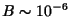 G.
G.
- The magnetic field of a neutron star can not be due to the ferro-magnetism of the irons on
its surface. Explain.
- What is the range of nuclear forces (in terms of fundamental constants)? Show that the
energy required for a nuclear reaction to occur by overcoming the Coulomb barrier is
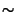 1 MeV.
1 MeV.
- The famous Solar neutrino problem refers to the fact that the observed number of
neutrinos are smaller than that expected from the Sun. What is the reaction that gives
rise to these neutrinos? Is this a fast or a slow reaction?
- Explain why heavier stars have a shorter life-time.
- Estimate the radius of a nucleus made up of
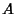 nucleons, assuming close-packing.
nucleons, assuming close-packing.
- What is the physical significance of the Gamow peak in nuclear reactions?
- Make a schematic plot of the energy densities of the matter and the radiation vs. time,
showing the temperature dependence of each of them.
Problems : 5 x 2 = 10
- The main signature of neutral hydrogen is the 21-cm line, which is the characteristic
of hyperfine transition. Estimate the energy of this hyperfine transition in atomic
hydrogen and check whether your answer has the correct order of magnitude value.
- A main sequence star and a giant star have the same effective temperature but the radius
of the giant is 50 times that of the main sequence star. If the two stars are at the same
distance from the earth, calculate the differences in their magnitudes.
Sushan Konar
2004-03-23